center of mass physics

Center of mass Physics

Today our topic is center of mass Physics. This topic is very important to understand better Physics. Without understanding concept of center of mass Physics, It will not be easy for you to understand better Physics, So try to understand center of mass physics.

In previous post we have already study center of mass basic concept for continuous mass distributed body. You can refer previous post Center of mass formula .But here we will study center of mass for hollow and solid hemisphere with easy concept.   

What is center of mass Physics ?

Center of mass of  a body is that point where whole mass of the body is concentrated it can lie within the body or outside the body depends upon the shape of the body.

Why need to study center of mass Physics ? 

In Practical every rigid body has some shape and size . If the body comes in motion then every point on rigid body have different velocity and acceleration. 

Suppose a rigid body of some mass m is rotating about its axis as well as translate. Every point on rigid body will have different velocity and acceleration.

It is really difficult to calculate velocity and acceleration of all point on rigid body.

Hence there is a single point where whole mass is concentrated is called center of mass and that point velocity and acceleration is consider as whole body velocity and acceleration.

Hence that special point is called center of mass.

We know that Newton's second law . Fnet = ma, p = mv. Here in this case "a" and "v"  is acceleration of center of mass  and "v" velocity of center of mass. If any body do combined motion rotational and translational then its path analysis will be easy, When we sit on center of mass and analyse body other particle motion.

Generally center of mass path is easy like (straight line, Circle, Projectile)       

Hence you can think the importance of center of mass.

Fnet  = ma equation has two important condition

Here "a" is acceleration of center of mass and m is a point mass.This is reason we need to study center of mass physics.

Practical uses and Application of center of mass Physics 

The center of mass plays an important role in astronomy. The barycenter is the point between two objects where they balanced each other. 

It is the center of mass where two or more celestial bodies orbit each other. When a moon orbits a planet or a planet orbits a star, both bodies are actually orbiting around a point that lies away from the center of the large bodies.

For example the moon does not orbit the exact center of the earth but a point on a line between the center of the earth and the moon, approximately 1710 km below the surface of the earth. Where their respective masses are balanced. This is the point about which the earth and moon orbits.

Automotive applications  engineers try to design sport car so that its center of mass is lowered to make the car handle easy.

Also uses in aeronautic, high jumping .

Now i think you have understand the importance of center of mass.

How to find hollow hemispherical center of mass ? 

                                                               

Center of mass hollow hemisphere

                                                                     

From the figure it is clear that mass is distributed over the surface area of hollow hemisphere. One thing is clear that hollow hemisphere is symmetric about x axis means positive x axis (right side) and negative x axis (left side) mass distribution is same. 

Hence Xcm will no need to calculate it will be at origin for Xcm.

Along y axis its mass is different for different value of y.

Let total mass of hollow hemisphere is M and its radius is R, Now taking a elemental ring of mass dm, now the thickness of elemental ring will be Rdϴ as shown in figure.

Now the radius of elemental ring is Rcosϴ  as shown above figure. Now the Ring above the origin that is y = Rsinϴ as shown in figure.

Ycm  = ∫ ydm/∫dm  now put the value of y  =  Rsinϴ 

Now dm can't be integrated, Because  dm is not written in terms of y, Hence we need to find out the mass of elemental dm first.

So to find out the mass of elemental ring, we have to consider surface mass density. which is define as mass per unit surface area, It is denoted by 𝞼 .

Hence  𝛔  = M/A = M/2𝛑R²   Since mass is only distribute on surface area of hollow sphere 

So we can write 𝛔 =dm/dA or dm  = 𝛔dA.

Now we can calculate the area of elemental ring and it will be area .

of elemental circle of radius Rcosϴ and thickness Rdϴ.

Hence Area = 2𝛑Rcosϴ*Rdϴ So for elemental area  dA =   2𝛑Rcosϴ*Rdϴ  hence from here dm = 𝛔*2𝛑Rcosϴ*Rdϴ.

Now use the equation for Ycm  = ∫ ydm/∫dm  = ⎰Rsinϴ *𝛔*2𝛑Rcosϴ*Rdϴ/M 

Here ∫dm = M  since total mass is M.

Ycm  = R³*𝛔*𝛑*1/M⎰2sinϴ*cosϴdϴ now putting value of 𝛔 and 2sinϴ*cosϴ = sin2ϴ then 

Ycm  = R³xM/2𝛑R²x𝛑/M⎰sin2ϴdϴ now take limit from 0 to 𝛑/2 total mass will be cover hence after simplification we will get .

                   𝛑/2 

Ycm  = R/2⎰sin2ϴdϴ

                  0

                               𝛑/2

Ycm  = R/2⎡-cos2ϴ/2⎤   now put the value we will get 

                                  0

 Ycm  = R/2 (2/2) = R/2  , Ycm = R/2 

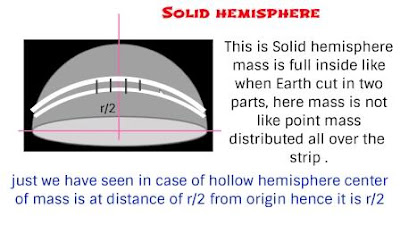
Center of mass for solid hemisphere  

Solid hemisphere can be made by many hollow hemisphere so we will use this technique to find the center of mass for solid hemisphere.

                                                           

This is 3-D because it is solid lets suppose an elemental strip is taken from origin at a r distance then just we have seen in case of hollow hemisphere its center of mass is at r/2 distance from origin.

Hence this elemental strip center of mass will be at r/2 distance from origin as shown above figure 

Now apply center of mass formula  Ycm  = ∫ ydm/∫dm .

Here it is clear y = r/2 

now this is solid so its mass density will be mass per unit volume and it is denoted by 𝛒 

  𝛒  = M/V  = M/(2x𝛑r³)/3 = 3M/2x𝛑r³  since half volume of solid sphere 

Ycm  =  ⎰r/2dm/⎰dm  = ⎰r/2dm/M  ⎰dm = M.

Since total mass is M

now for dm mass dm/dv  =𝛒  or dm  = 𝛒dv 

now for dv  = Area x thickness  = 2𝛑r²xdr

dm  = 𝛒2𝛑r²dr  now put the value in above equation we will get 

Ycm  = ⎰r/2x𝛒2𝛑r²drx1/M  =  put  𝛒 = 3M/2𝛑r³

            R

Ycm = ⎰r/2*3M/2𝛑r³*2𝛑r²dr/M  after simplification and integration we will get 

           0

Ycm  =   3R/8 

Now we will continue in next post. I hope you have enjoyed learning Center of mass Physics .If you like comment and share thanks for learning and share.

Dated 3rd Nov 2018