Gravitational potential energy
Gravitational potential is very important concept because the same concept is used in electric potential, So potential is a general concept, Which you need to understand the concept behind potential. Whenever you see gravitational potential then you must remember, the existence of gravitational potential is due to mass.
If mass is not present then gravitational potential will not exist, Can you think why ? well if there is no mass then there is no gravitational field and if no gravitational field then there is no gravitational potential.
So you can think potential depends upon field, which may be gravitational field or electric field or magnetic field in general but here you will learn about gravitational field potential.
If you have not studies gravitational field then i will suggest you first to learn about gravitational field in my previous post so that you can better understand gravitational potential concept, You can refer link Gravitational field.
When you see electric potential this is due to charge, but the potential concept for both the cases is same. Hence you will learn in this topic, what is potential ? and how it is calculated, why need to learn potential ? and then potential energy.
What is gravitational potential ?
Potential word itself has not got any defined meaning, whereas potential difference is defined as "the difference in potential between two points that represents the work involved or the energy released in the transfer of unit quantity of mass from one location to the other location". So it is clear that potential is a characteristics of location or point.
Suppose there are two points A and B and a small mass m is kept at point B, now this small mass m bringing from point B to A, now you need to do some amount of work that amount of work is called potential difference between B to A.
←m
Mathematically written as Va - Vb = (Work done B to A)/m A W B
with no change in kinetic energy, means when you are bringing mass m from point B to A the speed of mass does not change during the journey from B to A.then only this formula is valid.
Potential at a point
As i have stated potential itself is not a defined meaning in Physics, So we have taken a reference point, such that the potential of reference point will be zero. Now you can compare any new point potential from that reference point, like how much is potential at new point.
Hence reference point was take at infinity (∞) so potential at infinity is zero, now you are able the compare any new point potential respect to infinity potential. But remember point does not have energy but whenever you bring a mass near to that point then energy is stored in mass.
So it is clear that energy is available in mass but potential at point or at location indicate how much energy will be available at that location in the body or mass, which is bring to that point. You must remember every point has some potential, If you bring a mass then energy is stored in mass, If you don't bring the mass then energy is not stored, but potential is always there.
You generally listen the peoples use potential word like, there is potential in this business, what do you understand by using this word ? Well that person is indicating about money in that business, Hence money is form of energy in Physics.
So potential indicate about energy of at point or location but when you bring a mass.
So it is clear that energy is available in mass but potential at point or at location indicate how much energy will be available at that location in the body or mass, which is bring to that point. You must remember every point has some potential, If you bring a mass then energy is stored in mass, If you don't bring the mass then energy is not stored, but potential is always there.
You generally listen the peoples use potential word like, there is potential in this business, what do you understand by using this word ? Well that person is indicating about money in that business, Hence money is form of energy in Physics.
So potential indicate about energy of at point or location but when you bring a mass.
Now from the above two point, which you have taken A and B put point B at infinity that is B(∞), now put a small mass m at infinity and bring this mass to point A, the work done will give you the potential at point A.
Now you can write mathematically VA - V∞ = (Work done infinity to A)/m put V∞ = 0 then you will get VA = (Work done W infinity to A)/m .
what is VA ? this is potential at point A.
Actually potential at a point does not exist, we are just comparing from infinity point potential so you are able to define potential at point A.
Hence potential at a point is define as work done per unit mass bringing from infinity to that point A, such that without changing the kinetic energy of mass m means mass moving very very slowly from infinity to point A.
Now i hope your concept about potential and potential difference is clear.
Gravitational potential due to a mass M
As from the above figure Earth has created its gravitational field surround to it in all direction as shown in figure, gravitational field g its direction is directed towards the Earth centre, So any mass comes in gravitation field attracted and fall towards the centre of the Earth.Now you can find gravitational potential at any point near and above the Earth surface due to mass of Earth.
All different location in field gravitation potential will be different.
Now suppose there is no any mass and you want to find potential at a point P, then what will you do ? as per definition of potential a small mass m will bring from infinity to that point P and the amount of work done per unit mass will be potential at point P.
But think if there is no any mass then you will required to do any work to bring small mass m from infinity to point P, See the definition of potential at a point state that the amount of work done per unit mass required to bring small mass to point P will be potential at point P.
But first of all you need to check whether that work is required or not, So can you tell me in this case work is required or not ,well answer is BIG no think why ?
See when you will touch the small mass m at infinity then according to Newton's first law every object try to continue in rest or uniform motion unless and until external applied force is zero.Hence see in this case there is no any external force on small mass m, So it will start motion after touching very very little force and it will continue in uniform motion.
Also there is no any attractive force for small mass m because there is no any mass.
two important point first it should reach the point P and second its speed must not change during the journey from infinity to point P.
Hence you see both the point are valid in this case, It will reach itself point P without doing any external work as well as without changing the speed.suppose the friction and air resistance is neglected.
Now when you are not doing work to bring small mass m, then how it will stop at point P, for this you just touch and stop at point P it will stop easily, this stooping and touching force will be very very small and consider as negligible.
Hence potential at point P will be zero, So it is not necessary that all point will have some potential, it depends upon mass. See the below picture.
From the above figure see the second case, there is now a mass M so small mass will be attracted towards the heavy mass M due to gravitation force.
Now you have to work to bring this small mass m slowly otherwise the speed of mass m will increase which we don't want ,so you have to apply force against this gravitation force and this work done will be by external agent.
Now suppose point P is at a distance r from the heavy mass M Hence in this case potential at point P will be Vp = -GM/r potential is a scalar quantity, negative sign indicates here small mass m is bounded by big mass M so sign is negative.
In other words you can say the work done by external agent is negative how ? well see you are applying the force against gravitational force and displacement is in opposite direction so the work done by external agent will be negative.Gravitational potential is always negative.
So mass create potential at any point. If mass will not be present then potential will not be available at any point .Now i hope your concept is clear about gravitational potential due to a mass.
Derivation of potential due to mass at a point
Suppose a heavy mass M as shown in above picture case 2, you want to find potential at point P at a distance r from heavy mass M.
let at x distance bring small mass m from point P then gravitational force between M and m will be GMm/x² , see here gravitational force is variable depending upon x so you know that variable work done is calculate as.
∞ ∞ ∞
W = ∫F.dx = ∫ Fdxcos180 = -∫GMmdx/x² = -GMm∫x⁻²dx =GMm/r now this work done
r r r
from Point P to ∞ hence work done from ∞ to point P will be -GMm/r
W = -GMm/r
Now potential at point P is defined as Vp = ( work done from ∞ to P )/m so
Vp = -GMm/mr = -GM/r so Vp = -GM/r.
Now from question Q1 find the potential at point P due to all three masses .
Ans you know that due to mass m potential formula is given as V = -Gm/r , where r is distance from mass to point p.
So first calculate the distance AP = BP = CP , now from triangle APcos30 = a/2
APx√3/2 = a/2 or AP = a/√3 , Hence BP = a/√3, CP = a/√3 now potential due to single mass m at point P will be V = -Gm/(a/√3) = -Gm√3/a .
potential is scalar quantity so due to all three mass potential will be same at point P
Hence total potential at point P will be three times Vtotal = -3xGm√3/a = -3√3Gm/a .
Now from question Q2 above picture, You have to find the work done during moving small mass m from point A to point B.
Ans Here m<
VB - VA = (work done from A to B)/m.
Hence (Work done from A to B) = m(VB- VA) , VB = -GM/4x , VA = -GM/2x so put the value to find work done.
(Work done from A to B) = m(-GM/4x - (-GM/2x)) = mGM(1/2x - 1/4x) = mGM/4x
(Work done from A to B) = mGM/4x .
See the numerical question below.
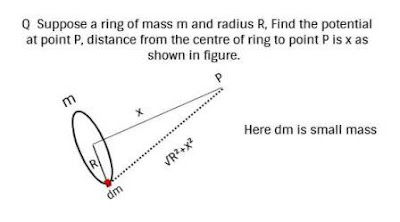
As from question this is ring so it is not a point mass, but whatever formula derived for potential is only applicable for point mass.
Remember in this case you can't assume the whole mass of ring concentrated at centre of ring, because it is extended mass and formula for potential is inversely proportional to distance.
Hence to solve the problem you have to divide ring mass in many small masses as shown dm and after that for addition of this all masses, you know just integrate whole masses.
So potential at point P due to dm mass will be ∫ dVp = -G∫dm/(√R²+x² )
Now here R and x are also constant and ∫dm = m
So Vp = -Gm/(√R²+x²) .
Now suppose if this point is very very far distance just feel then ring will look like a point mass, because radius will not look so R→0 so in this case Vp = -Gm/x .
Now what will be potential at centre of ring, gravitational field will be zero but potential will not be zero, at centre of ring put x =0 then you will get Vp = -Gm/R .
So in this way you can solve numerical problem, If there may be two ring separated with some distance and ask the potential at axis of ring you can find at any point due to both rings.
In previous post i have discussed in details about gravitational field and link is given above in first paragraph, you can refer. Gravitational potential discussed in this post, Now you will see the relation between these two quantity. This is important relation you must remember it will also help you to solve numerical problems.
→
Gravitational field E is a vector quantity and gravitational potential V is a scalar quantity.
Gravitational field is property of a Mass whereas potential is a characteristics of a point or location. Now the relation between gravitational field and gravitational potential is given as
→
E = -dV/dr where dV/dr indicate differentiation of gravitational potential with respect to position vector. You can also write Ex = -𝜕v/𝜕x, Ey = -𝜕v/𝜕y , Ez = -𝜕v/𝜕z partial differentiation of potential along x, y, and z axis because gravitational field is a vector quantity.
Potential is not along x,y and z direction because you know potential is a scalar quantity so it has no any direction. Now you can check the above formula.
You know potential at a point P, x distance due to mass M Vp = -GM/x.
use Ex = -𝜕v/𝜕x = -𝜕(-GM/x)/𝜕x = GM𝜕(x⁻¹)/𝜕x = -GM/x² Ep = -GM/x here negative sign in field indicate direction is towards the mass M centre.
→
Hence E = -dV/dr is correct formula.
See from the figure E a gravitation field, you know that in a field if you place a mass then gravitational force mE will act on mass towards the field direction as shown.
Now to move the mass m from point A to B, you have to apply very little greater force in opposite direction Fext (external force) -mE negative sign indicate opposite direction.
Now work done by external force Wext = force*displacement = -mEr , this work done bringing mass m from point A to B.
Again recall potential difference VB - VA = (work done A to B)/m , now put the value of work done, so you will get.
VB - VA = -mEr/m = -Er , Now if i told you A is very very close to B then r will be dr and VB - VA will be dV , hence you can write .
dV = -Edr or E = -dV/dr hence it proved.
I will continue post with more concept. I hope you have enjoyed learning gravitational potential energy. I want your feedback through comment, like and share, learn and grow thanks for sharing .
Ans you know that due to mass m potential formula is given as V = -Gm/r , where r is distance from mass to point p.
So first calculate the distance AP = BP = CP , now from triangle APcos30 = a/2
APx√3/2 = a/2 or AP = a/√3 , Hence BP = a/√3, CP = a/√3 now potential due to single mass m at point P will be V = -Gm/(a/√3) = -Gm√3/a .
potential is scalar quantity so due to all three mass potential will be same at point P
Hence total potential at point P will be three times Vtotal = -3xGm√3/a = -3√3Gm/a .
Now from question Q2 above picture, You have to find the work done during moving small mass m from point A to point B.
Ans Here m<
VB - VA = (work done from A to B)/m.
Hence (Work done from A to B) = m(VB- VA) , VB = -GM/4x , VA = -GM/2x so put the value to find work done.
(Work done from A to B) = m(-GM/4x - (-GM/2x)) = mGM(1/2x - 1/4x) = mGM/4x
(Work done from A to B) = mGM/4x .
See the numerical question below.
As from question this is ring so it is not a point mass, but whatever formula derived for potential is only applicable for point mass.
Remember in this case you can't assume the whole mass of ring concentrated at centre of ring, because it is extended mass and formula for potential is inversely proportional to distance.
Hence to solve the problem you have to divide ring mass in many small masses as shown dm and after that for addition of this all masses, you know just integrate whole masses.
So potential at point P due to dm mass will be ∫ dVp = -G∫dm/(√R²+x² )
Now here R and x are also constant and ∫dm = m
So Vp = -Gm/(√R²+x²) .
Now suppose if this point is very very far distance just feel then ring will look like a point mass, because radius will not look so R→0 so in this case Vp = -Gm/x .
Now what will be potential at centre of ring, gravitational field will be zero but potential will not be zero, at centre of ring put x =0 then you will get Vp = -Gm/R .
So in this way you can solve numerical problem, If there may be two ring separated with some distance and ask the potential at axis of ring you can find at any point due to both rings.
Relation between gravitation field (E) and gravitational potential (V)
In previous post i have discussed in details about gravitational field and link is given above in first paragraph, you can refer. Gravitational potential discussed in this post, Now you will see the relation between these two quantity. This is important relation you must remember it will also help you to solve numerical problems.
→
Gravitational field E is a vector quantity and gravitational potential V is a scalar quantity.
Gravitational field is property of a Mass whereas potential is a characteristics of a point or location. Now the relation between gravitational field and gravitational potential is given as
→
E = -dV/dr where dV/dr indicate differentiation of gravitational potential with respect to position vector. You can also write Ex = -𝜕v/𝜕x, Ey = -𝜕v/𝜕y , Ez = -𝜕v/𝜕z partial differentiation of potential along x, y, and z axis because gravitational field is a vector quantity.
Potential is not along x,y and z direction because you know potential is a scalar quantity so it has no any direction. Now you can check the above formula.
You know potential at a point P, x distance due to mass M Vp = -GM/x.
use Ex = -𝜕v/𝜕x = -𝜕(-GM/x)/𝜕x = GM𝜕(x⁻¹)/𝜕x = -GM/x² Ep = -GM/x here negative sign in field indicate direction is towards the mass M centre.
→
Hence E = -dV/dr is correct formula.
See from the figure E a gravitation field, you know that in a field if you place a mass then gravitational force mE will act on mass towards the field direction as shown.
Now to move the mass m from point A to B, you have to apply very little greater force in opposite direction Fext (external force) -mE negative sign indicate opposite direction.
Now work done by external force Wext = force*displacement = -mEr , this work done bringing mass m from point A to B.
Again recall potential difference VB - VA = (work done A to B)/m , now put the value of work done, so you will get.
VB - VA = -mEr/m = -Er , Now if i told you A is very very close to B then r will be dr and VB - VA will be dV , hence you can write .
dV = -Edr or E = -dV/dr hence it proved.
I will continue post with more concept. I hope you have enjoyed learning gravitational potential energy. I want your feedback through comment, like and share, learn and grow thanks for sharing .
Dated 6th Jan 2019





No comments:
Post a Comment